0%
April 22, 2022

WGAN and WGAN-GP

deep-learning

Contents

Results

After the implementation and the results I was amazed by the horrible performance of WGAN-GP compared to that of WGAN.

Although mnist is a toy dataset, but among all the GANs I have implemented none of them can converge that quickly even without tuning parameters for many times.

By WGAN Using 4000 Batches
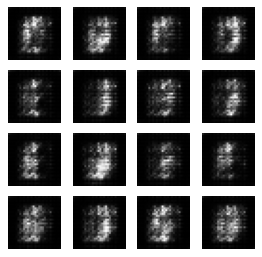
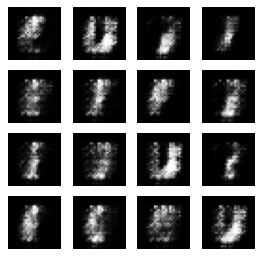
By WGAN-GP Using less than 1000 Batches

Wasserstein Metric

Definitions, Basic Examples and some Mathematics

Given the real distribution of real data, we try to approximate it by a distribution , such that for some network with being an unknown random variable (usually this is constructed from Gaussian distribution ).

From [MA] the Wasserstein metric behaves the best from experiment and theoretical observations:

where for any probability measures on , denotes the set of all transportation plans form to such that and . Here 's are canonical projections.

By an abuse of notation, for any probability measure that is absolutely continuous w.r.t. Lebesuge measure on we refer also the density function and write interchangeably, therefore and in our case, and thus the notation makes sense.

The following example is taken from [MA], let's fill in the detail:

Example. Let be a random variable sampled from uniform distribution on , the sets and form a disjoint subsets in .

Consider , denote the distribution of in and that of in , then and obviously have no nonempty common support.

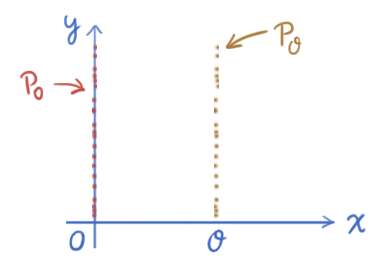
We consider the following metrics among these two distributions:

  • Reason. is obvious, for equality define the map on and on , then satisfies .

    From standard result in optimal transport, the map induces a transportation plan which is a measure on .

    Denote , we have

    therefore .

  • , where

    Reason. , since on which and have no common support, therefore

    Similarly, , and the result follows.

  • Reason. Demoninator 0 on a set of positive measure.

The Usual form of Wasserstein Metric for Coding

A remarkable result named Kantorovich-Rubinstein duality from optimal transport states that

Since , we can further write

where we assume that , for some density with being the latent dimension which we need to search by experiment (rigorously the equality holds by a standard real analysis trick: prove it for first characteristic functions, second simple functions, finally use monotone convergence etc).

WGAN Version

In coding we transform the last equality into an approximated form in

We will be replacing the set of 1-Lipschitz functions by a parametrized family and perform the following in train loop:

  • Line 6 in Algorithm.

    • We minimize the term

      in the RHS of w.r.t. to get a result that is hopefully close to .

    • We update critic by .

  • Line 11 in Algorithm.

    • We minimize
      in the RHS of w.r.t. to get smaller .
    • We update generator by .

  • Usually the candidates of are modified from our discriminator.

  • (cont'd) As we will not use signmoid output any more, usually we call a critic which replaces the role played by the usual trick. Then we can modify our discriminator to output any tensor of shape .

WGAN-GP Version

As discussed in [IG] the weight clipping causes our critics to learn very simple functions, therefore we remove the constraint on the norm of for and force the norms to be bounded by introducing a loss term in the following:

Where denotes the uniform distribution of points along straight lines between any pair of points from and ,

  • The first term is the old critic term that we need to minimize in order to approximate the Wasserstein distance.
  • The second term will be mininized w.r.t. to control the growth of the gradients of .

  • Line 7 in Algorithm. We minimize
    w.r.t. , where denotes critic, we will take .
  • (cont'd) We update the critic by .
  • Line 12 in Algorithm. Update of generator remains the same, we still minimize
    w.r.t. .
  • (cont'd) We update the generator by .
  • No BatchNormalization in critic, instead we use LayerNormalization.
  • Remove weight-clipping.
  • We use smaller learning rate.
  • Anything else remain the same.

Implementation of WGAN

Constants

With exactly the same setup as in DCGAN, we edit the following constants:

img_rows = 28
img_cols = 28
channels = 1
weight_clip = 0.01
batch_size = 64
critic_iteration = 5
img_shape = (img_rows, img_cols, channels)
learning_rate = 1e-5
z_dim = 128
Critic

We have the same generator, but different discriminator, which we call critic as it no longer output a number in :

gen = build_generator()
critic = build_critic()

def build_critic():
    model = Sequential()
    model.add(
        Conv2D(32,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same')
        )
    model.add(LeakyReLU(alpha=0.01))
    model.add(
        Conv2D(64,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU(alpha=0.01))
    model.add(
        Conv2D(128,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same'))
    model.add(BatchNormalization())
    model.add(LeakyReLU(alpha=0.01))
    model.add(Flatten())
    model.add(Dense(1))

    return model
Train Loop with Wasserstein Metric in Place of the Adversarial Loss
def train(iterations, batch_size, sample_interval):
  (x_train, _), (_, _) = mnist.load_data()
  x_train = x_train/127.5 - 1.0
  # np.shape(x_train) = (60000, 28, 28), for conv2D we need the channel dimension at the last axis
  x_train = np.expand_dims(x_train, axis=3)

  gen_opt = RMSprop(lr=learning_rate)
  critic_opt = RMSprop(lr=learning_rate)

  for i in range(iterations):
    print(f"iteration: {i+1}", end = "\r")

    for j in range(critic_iteration):
      z = tf.random.normal((batch_size, z_dim), 0, 1)

      update_gen = ((j+1) % (critic_iteration)) == 0

      with tf.GradientTape() as critic_tape, tf.GradientTape() as gen_tape:
        idxs = np.random.randint(0, x_train.shape[0], batch_size)
        imgs = x_train[idxs]
        gen_imgs = gen(z, training=True)

        critic_fake = critic(gen_imgs)
        critic_real = critic(imgs)
        loss_critic = -(tf.math.reduce_mean(critic_real) - tf.math.reduce_mean(critic_fake))

        if update_gen:
          loss_gen = - tf.math.reduce_mean(critic_fake)

      grad_of_critic = critic_tape.gradient(loss_critic, critic.trainable_variables)
      critic_opt.apply_gradients(zip(grad_of_critic, critic.trainable_variables))

      weights = critic.get_weights()
      weights = [tf.clip_by_value(w, -weight_clip, weight_clip) for w in weights]
      critic.set_weights(weights)

      if update_gen:
        grad_of_gen = gen_tape.gradient(loss_gen, gen.trainable_variables)
        gen_opt.apply_gradients(zip(grad_of_gen, gen.trainable_variables))

    if (i+1) % sample_interval == 0:
      iteration_checkpoints.append(i+1)
      sample_images(gen)

Finally:

iterations = 20000
sample_interval = 100

train(iterations, batch_size, sample_interval)

Implementation of WGAN-GP

There are just few modifications from WGAN, first for the constants:

New Constants
img_rows = 28
img_cols = 28
channels = 1
batch_size = 64
critic_iteration = 5
img_shape = (img_rows, img_cols, channels)
learning_rate = 1e-4
z_dim = 128

We just decrease learning_rate and remove critic_iteration.

New Critic

We replace all BatchNormalization by LayerNormalization:

def build_critic():
    model = Sequential()
    model.add(
        Conv2D(32,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same')
        )
    model.add(LeakyReLU(alpha=0.01))
    model.add(
        Conv2D(64,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same'))
    model.add(LayerNormalization())
    model.add(LeakyReLU(alpha=0.01))
    model.add(
        Conv2D(128,
               kernel_size=3,
               strides=2,
               input_shape=img_shape,
               padding='same'))
    model.add(LayerNormalization())
    model.add(LeakyReLU(alpha=0.01))
    model.add(Flatten())
    model.add(Dense(1))

    return model
Gradient Penality

Next we define function to compute gradient penality:

def gradient_penality(critic, real_sample, fake_sample):
    epsilon = tf.random.normal([batch_size, 1, 1, 1], 0.0, 1.0)
    interpolated = epsilon * real_sample + (1 - epsilon) * fake_sample

    with tf.GradientTape() as gp_tape:
      gp_tape.watch(interpolated)
      critic_inter = critic(interpolated, training=True)

    grads = gp_tape.gradient(critic_inter, [interpolated])[0]
    norm = tf.sqrt(tf.reduce_sum(tf.square(grads), axis=[1, 2, 3]))
    penality = tf.reduce_mean((norm - 1.0) ** 2)
    return penality
New Train Loop

We remove weight-clipping and modify the weight update of critic by adding gradient penality:

def train(iterations, batch_size, sample_interval):
  (x_train, _), (_, _) = mnist.load_data()
  x_train = x_train/127.5 - 1.0
  # np.shape(x_train) = (60000, 28, 28), for conv2D we need the channel dimension at the last axis
  x_train = np.expand_dims(x_train, axis=3)

  gen_opt = RMSprop(lr=learning_rate)
  critic_opt = RMSprop(lr=learning_rate)

  for i in range(iterations):
    print(f"iteration: {i+1}", end = "\r")

    for j in range(critic_iteration):
      z = tf.random.normal((batch_size, z_dim), 0, 1)

      update_gen = ((j+1) % (critic_iteration)) == 0

      with tf.GradientTape() as critic_tape, tf.GradientTape() as gen_tape:
        idxs = np.random.randint(0, x_train.shape[0], batch_size)
        imgs = x_train[idxs]
        gen_imgs = gen(z, training=True)

        critic_fake = critic(gen_imgs, training=True)
        critic_real = critic(imgs, training=True)
        gp = gradient_penality(critic, imgs, gen_imgs)

        loss_critic = tf.math.reduce_mean(critic_fake) \
                      - tf.math.reduce_mean(critic_real) + 10 * gp

        if update_gen:
          loss_gen = - tf.math.reduce_mean(critic_fake)

      grad_of_critic = critic_tape.gradient(loss_critic, critic.trainable_variables)
      critic_opt.apply_gradients(zip(grad_of_critic, critic.trainable_variables))

      if update_gen:
        grad_of_gen = gen_tape.gradient(loss_gen, gen.trainable_variables)
        gen_opt.apply_gradients(zip(grad_of_gen, gen.trainable_variables))

    if (i+1) % sample_interval == 0:
      iteration_checkpoints.append(i+1)
      # print("%d [D loss: %f] [G loss: %f]" % (i + 1, loss_critic, loss_gen))
      sample_images(gen)

Reference