0%
July 25, 2021

Algorithm: Merge Sort and its Time Complexity

algorithm

Contents

Algorithms

The Merge Sort
def merge_sort(arr):
  if len(arr) == 1:
    return arr

  mid_index = int(len(arr)/2)

  L = arr[0:mid_index]
  R = arr[mid_index:]

  L = merge_sort(L)
  R = merge_sort(R)
  • The algorithm is locked and looped here until a return is resolved.
  • When merge_sort(len-1 array)'s return two sorted arrays to the previous call, L and R then merge into a len-2 array arr, and get returned.
  • Then the locked merge_sort(len-2 array)s' call continue, L and R then merge into a sorted len-4 array arr.
  • Similarly, the locked merge_sort(len-4 array)s' call return two sorted arrays separately, they then merge into a len-8 sorted array.
  head_L, head_R, i = 0, 0, 0

  while head_L < len(L) and head_R < len(R):
    if L[head_L] < R[head_R]:
      arr[i] = L[head_L]
      head_L += 1
    else:
      arr[i] = R[head_R]
      head_R += 1
    i += 1

  while head_L < len(L):
    arr[i] = L[head_L]
    head_L += 1
    i += 1

  while head_R < len(R):
    arr[i] = R[head_R]
    head_R += 1
    i += 1

  print(f"sorting L:{L} and R:{R}, result:{arr}")
  return arr

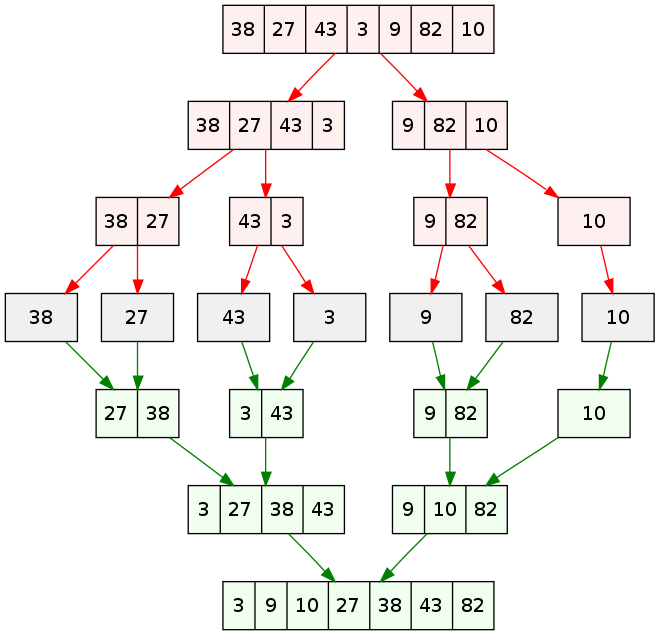
We try to sort the following and print log:

to_be_sorted = [2,10,5,100,66,24,27,30]
merge_sort(to_be_sorted)

which yields

sorting L:[2] and R:[10], result:[2, 10]
sorting L:[5] and R:[100], result:[5, 100]
sorting L:[2, 10] and R:[5, 100], result:[2, 5, 10, 100]
sorting L:[66] and R:[24], result:[24, 66]
sorting L:[27] and R:[30], result:[27, 30]
sorting L:[24, 66] and R:[27, 30], result:[24, 27, 30, 66]
sorting L:[2, 5, 10, 100] and R:[24, 27, 30, 66], result:[2, 5, 10, 24, 27, 30, 66, 100]
The Time Complexity

The algorithm in plain text:

  • We are bisecting our length- long array by half until the resulting array has length , which takes steps to complete. For each dividing steps, it takes exactly operations for cloning elements to the evenly divided pairs of arrays (L and R)'s. At the end of bisections, we get at most operations.

  • Starting from length-1 array, we merge pairs of adjacent arrays in the 3 while loops above, these triples of while loops in total take at most operations. But it just takes stages of steps to merge from length-1 array to length- array.

Therefore by summing up, the time complexity of merge sort is .