0%

Implement ECDSA for Transaction Verification in a Blockchain

October 8, 2025

Blockchain

Elliptic-Curve

Rust

Contents

1. Repository

Executable testing code is placed at:

This project is a study of Rust under the block-chain context, and this is not a full block-chain project.

2. Cargo.toml

hex = "0.4.3"
p256 = {version  = "0.13.2", features=["ecdsa", "arithmetic"]}
rand_core="0.6"
sha2 = "0.10.9"
ripemd160 = "0.9"
bs58 = "0.4"
serde={version="1.0.207", features=["derive"]}
serde_json = "1.0.124"

3. Crate

use bs58;
use p256::ecdsa::{
    Signature, SigningKey, VerifyingKey,
    signature::{self, SignerMut, Verifier},
};
use rand_core::OsRng;
use ripemd160::{Digest as RipDigest, Ripemd160};
use serde::Serialize;
use sha2::{Digest, Sha256};

  • Here we import the traits SignerMut and Verifier simply for importing the implementation for the struct VerifyingKey.

  • More specifically, without Verifier the method call

    public_key.verify(&msg_bytes, &signature)

    will throw an error in IDE level, where public_key: VerifyingKey<NistP256>.

4. Define Wallet and Transaction

// src/wallet/mod.rs

pub struct Wallet {
    pub signing_key: SigningKey,
    pub verifying_key: VerifyingKey,
    address: String,
}

#[derive(Serialize, Debug, Clone)]
pub struct Transaction {
    pub sender: String,
    pub recipient: String,
    pub amount: u64,
    pub public_key: String,
    pub signature: String,
}

5. ECDSA Wallet Implementation: Signing and Verifying Transactions

5.1. Detail Hidden in Crate p256, ripemd160 and OsRng
5.1.1. More on public key and private key in an elliptic curve setting

Let's start our long journey from defining the factory method of a Wallet:

1impl Wallet {
2    pub fn new() -> Self {
3        let signing_key = SigningKey::random(&mut OsRng);
4        let verifying_key = signing_key.verifying_key().clone();
5        let mut address = String::new();

Recall that the p256 curve (also known as secp256r1 or prime256v1 or 256-bit prime field) has these parameters:

a = -3
b = 0x5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B
p (prime field) = 2^256 - 2^224 + 2^192 + 2^96 - 1

What OsRng provides is just the random number generation for creating private keys. The process works like this:

  1. The curve parameters below are fixed in p256 (that's why we import SigningKey from it)
    • prime
    • a generator on the elliptic curve
    • an order
  2. OsRng generates a random number between and as a private key
  3. The public key (i.e., verifying_key) is calculated as
  4. From coding perspective the actual verifying_key that we use is the concated string of the coordinates [Q_x, Q_y].
5.1.2. Isn't a private key just an integer? Why need SigningKey

Essentially private key is just a random number in ( the order of a cylic group fixed in p256), we wrap it into a struct created by SigningKey::random to provide a safe abstraction that:

  • Ensures the random number is in the correct range
  • Prevents common cryptographic mistakes
  • Handles the complexities of ECDSA operations (such as creating verifying_key and signing a json payload in string)

Full Implementation of SigningKey includes:

  • The actual private key (the random number we just picked)
  • Methods for signing (sign)
  • Methods for deriving the public key in above (the verifying_key)
  • Proper serialization/deserialization
5.2. Generate an address

We continue to implement the factory method of a Wallet. Let's define a mutable closure to mutate the address just defined in line 5.

6        let mut gen_address = || {
7            let key_points = verifying_key.to_encoded_point(false);
8            if let (Some(x), Some(y)) = (key_points.x(), key_points.y()) {
9                let mut pub_key_bytes = Vec::with_capacity(x.len() + y.len());
10                pub_key_bytes.extend_from_slice(x);
11                pub_key_bytes.extend_from_slice(y);
12                let hash = Sha256::digest(&pub_key_bytes);
13                let mut hasher = Ripemd160::new();

See Remark 11 for the difference between Sha256 and Ripemd160.

14                hasher.update(&hash);
15                let mut address_hash_result = hasher.finalize().to_vec();
16                address_hash_result.insert(0, 0x00);

See Remark 22 below for the purpose of 0x00.

17                let hash2 = Sha256::digest(&address_hash_result);
18                let hash3 = Sha256::digest(&hash2);
19                let checksum = &hash3[0..4];
20                let full_hash = [address_hash_result, checksum.to_vec()].concat();
21                address = bs58::encode(full_hash).into_string();
22            } else {
23            }
24        };
25
26        gen_address();
27
28        Self {
29            signing_key,
30            verifying_key,
31            address,
32        }
33    }

Next we print out private and public key in hexadecimal representation as string.

34    pub fn private_key_str(&self) -> String {
35        hex::encode(self.signing_key.to_bytes())
36    }
37
38    pub fn public_key_str(&self) -> String {
39        let key_points = self.verifying_key.to_encoded_point(false);
40        if let (Some(x), Some(y)) = (key_points.x(), key_points.y()) {
41            let pub_str = hex::encode(&x).as_str().to_string() + hex::encode(&y).as_str();
42            pub_str
43        } else {
44            String::new()
45        }
46    }
47
48    pub fn get_address(&self) -> String {
49        self.address.clone()
50    }

Note that the direct concatenation of the hex strings of x,y-coordinate of the public key in line 41 is known as uncompressed key. We need to know this detail when we try to verify the transaction by the public key.

5.3. Create a Signature for a Transaction
5.3.1. Step 1. Convert transaction into json string
51    pub fn sign_transaction(&mut self, receiver: &String, amount: u64) -> Transaction {
52        let mut transaction = Transaction {
53            sender: self.address.clone(),
54            recipient: receiver.clone(),
55            amount,
56            signature: String::new(),
57            public_key: self.public_key_str(),
58        };
59        let serialized_str = serde_json::to_string(&transaction).unwrap();
5.3.2. Step 2. Sign the json string
60        let serialized_bytes = serialized_str.as_bytes();
61        let signature: Signature = self.signing_key.sign(serialized_bytes);
62        transaction.signature = hex::encode(signature.to_bytes());
63        transaction
64    }

By creating a signature in line 61 we mean that

  1. We hash the message (arbitrary length) into a 32 bytes value by sha256
  2. This hashed value is treated as an integer in 32 bytes, we do subsequent computation in 256-bit prime field to create a pair of two 32 bytes value (interchangeably in bytes or String).

We will discuss more on the values in the next section.

Note that when we try to verify the signature with the message (in our case, the transaction), we need to return the transaction.signature to an empty string. We will see that in line 67 below.

5.4. Verify the Signature to Justify the Transaction is Valid
5.4.1. Step 1. Get the hashed transaction payload H(m)
65    pub fn verify_transaction(transaction: &Transaction) -> bool {
66        let mut transaction_clone = transaction.clone();
67        transaction_clone.signature = String::new();
68
69        let message = serde_json::to_string(&transaction_clone).unwrap();
70        let msg_bytes = message.as_bytes();

This finishes the part to create a message to verify.

5.4.2. Step 2. Reconstruct Signature<NistP256> from the signature

Recall that from study notes on elliptic curve, a signature is a pair of two 32 bytes value (String or [u8; 32]) [R | S] computed from (backend) client side:

Here

  • denotes the x-coordinate of point in , where

  • is a generator of the cyclic subgroup in the elliptic curve

  • is a nounce, a randomly selected integer for each transaction

  • H(m): [u8, 32] is implicitly calculated via line 61 using sha256, this value is completely hidden from us and buried into the value S in the signature [R | S].

    In computation H(m) is converted into BigInt for mathematical computation of S on an p256-elliptic curve.

Now line 71 to 73 becomes very clear to us:

71        let signature = transaction.signature.clone();
72        let signature_bytes = hex::decode(signature).unwrap();
73        let signature_array: [u8; 64] = signature_bytes.try_into().unwrap();

try_into is a special trick/methodology in rust for type casting when we have a type declared on the left hand side. We do an unwrap() since it returns a Result enum.

74        let signature = match Signature::from_bytes(&signature_array.into()) {
75            Ok(signature) => signature,
76            Err(e) => {
77                println!("error: {:?}", e);
78                return false;
79            }
80        };
81        let public_key_str = transaction_clone.public_key.clone();
82        let mut public_key_bytes = hex::decode(public_key_str).unwrap();
83        public_key_bytes.insert(0, 0x04);

See Remark 33 for the purpose of 0x04.

5.4.3. Step 3. Undergo the mathematical validation

Recall that a verification of a message and a signature comprises of the following computation:

Where the key is directly taken from the payload of the transaction (line 81-83). From coding point of view is rephased as

with function signature

fn verify(&self, message: &[u8], &Signature<NistP256>) -> Result<()>

in line 85 below:

84        let public_key = VerifyingKey::from_sec1_bytes(&public_key_bytes).unwrap();
85        public_key.verify(&msg_bytes, &signature).is_ok()
86    }
87}

Note that &msg_bytes is hashed into [u8; 32] again internally and hidden from us.

6. main.rs

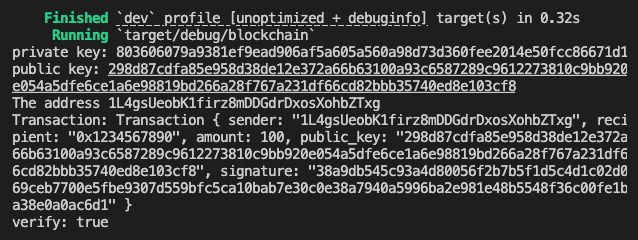
Finally we test the wallet and print the outcome for demonstration.

mod wallet;

use wallet::Wallet;

fn main() {
    let mut wallet = Wallet::new();
    println!("private key: {}", wallet.private_key_str());
    println!("public key: {}", wallet.public_key_str());
    println!("The address {}", wallet.get_address());
    let mut transaction = wallet.sign_transaction(&"0x1234567890".to_string(), 100);
    println!("Transaction: {:?}", transaction);
    transaction.amount += 0;
    println!("verify: {}", Wallet::verify_transaction(&transaction));
}

And we get the output:

7. References

8. Footnotes

  1. Remark 1. Note that this hasher from Ripemd160 does not share the same purpose as the hasher Sha256::new().

    1. SHA256
      • Outputs a 256-bit (32 bytes) hash
      • Generally considered more secure
      • Used in Bitcoin and many other cryptocurrencies
      • // Example:
let input = b"hello";
let hash = Sha256::digest(input);  // 32 bytes output
    2. RIPEMD160
      • Outputs a 160-bit (20 bytes) hash
      • Used specifically in Bitcoin address generation
      • Makes addresses shorter while maintaining security
      • // Example:
let mut hasher = Ripemd160::new();
hasher.update(input);
let hash = hasher.finalize();  // 20 bytes output
    ↩

  2. Remark 2. In cryptocurrency address generation (specifically Bitcoin-style addresses), the 0x00 prefix is added to indicate the network version or address type. Here's what it means:

    • 0x00 is the version byte for mainnet addresses in Bitcoin

    Different networks/coins use different version bytes:

    1. 0x00 Bitcoin mainnet
    2. 0x6f Bitcoin testnet

    Other cryptocurrencies use different values.↩

  3. Remark 3. The 0x04: u8 prefix is used in SEC1 (Standards for Efficient Cryptography) encoding for uncompressed public keys in elliptic curve cryptography.

    Other prefix values include:

    • 0x02 or 0x03 Used for compressed public key format
    • 0x02 Y coordinate is even
    • 0x03 Y coordinate is odd
      When is a solution, so is , thus we need 0x02 and 0x03 to identify the value.

    In the code, when we encode the public key, we start with the raw X and Y coordinates directly concatenated (line 41).

    Therefore we add 0x04 at the head to tell the decoder this is an uncompressed key, the resulting format is: [0x04 | X coordinate | Y coordinate].↩